Fun With Diffusion Models!

Overview

This project focuses on implementing a diffusion model to generate images. The diffusion model is a generative model that generates images by iteratively applying a series of transformations to a noise image. The model is trained to generate images that are similar to the training data. The project is divided into two parts. In Part 1, we implement the forward process of the diffusion model and explore different denoising techniques using a pre-trained diffusion model. In Part 2, we train a single-step denoising UNet and extend it to include time-conditioning and class-conditioning.

Octo… Dog 🐶			Octocat 😹

5A Part 0: Setup

In this part, we set up the environment and load the pre-trained diffusion model to generate images using seed 180.

We can see the quality of the generated images are quite good. They are highly correlated with the text prompts. However, there are some artifacts in the images. After increasing the number of inference steps, there is actually not much difference in the quality of the images. The defects in the images are still present.

5A Part 1.1: Implementing the Forward Process

In this part, we implement the forward process of the diffusion model.

t = 250	t = 500	t = 750

5A Part 1.2: Classical Denoising

In this part, we use the classical Gaussian blur filter to denoise the images.

	t = 250	t = 500	t = 750
Noisy
Gaussian Blur Denoised

5A Part 1.3: One-Step Denoising

In this part, we use the pre-trained diffusion model to denoise the images with one step.

	t = 250	t = 500	t = 750
Noisy
One-Step Denoised

5A Part 1.4: Iterative Denoising

In this part, we iteratively denoise the images with the pre-trained diffusion model.

The following images show the iterative denoising process at different time steps.

t = 690	t = 540	t = 390	t = 240	t = 90	t=0

We can see that the iterative denoising process can effectively denoise the image.

Original	Gaussian Blur Denoised	One-Step Denoised	Iterative Denoised

5A Part 1.5: Diffusion Model Sampling

In this part, we sample images from the diffusion model.

5A Part 1.6: Classifier-Free Guidance (CFG)

In this part, we use the classifier-free guidance to guide the diffusion model to generate images with the prompt “a high quality photo”.

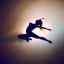We can see that the generated images have higher quality than the images generated without CFG.

5A Part 1.7: Image-to-image Translation

In this part, we’re going to take the original test image, noise it a little, and force it back onto the image manifold without any conditioning. i_start is the starting time step for the denoising process.

Campenile

i_start = 1	i_start = 3	i_start = 5	i_start = 7

i_start = 10	i_start = 20	i_start = 30	Original Image

Mong Kok

i_start = 1	i_start = 3	i_start = 5	i_start = 7

i_start = 10	i_start = 20	i_start = 30	Original Image

Victoria Harbour

i_start = 1	i_start = 3	i_start = 5	i_start = 7

i_start = 10	i_start = 20	i_start = 30	Original Image

5A Part 1.7.1: Editing Hand-Drawn and Web Images

In this part, we’re going to apply the SDEdit to nonrealistic images (e.g. painting, a sketch, some scribbles), making them look more realistic.

Hand-Drawn Image: Merry Cat-mas!

i_start = 1	i_start = 3	i_start = 5	i_start = 7

i_start = 10	i_start = 20	i_start = 30	Original Image

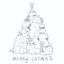Hand-Drawn Image: Monster

i_start = 1	i_start = 3	i_start = 5	i_start = 7

i_start = 10	i_start = 20	i_start = 30	Original Image

Web Image: Minecraft

i_start = 1	i_start = 3	i_start = 5	i_start = 7

i_start = 10	i_start = 20	i_start = 30	Original Image

5A Part 1.7.2: Inpainting

In this part, we’re going to implement inpainting. To do this, we can run the diffusion denoising loop. But at every step, after obtaining the denoised image, we can force the pixels that we do not want to change back to the original image.

	Campanile	Street	Victoria Harbour
Original
Mask
Inpainted

5A Part 1.7.3: Text-Conditional Image-to-image Translation

In this part, we will do the same thing as SDEdit, but guide the projection with a text prompt. This is no longer pure “projection to the natural image manifold” but also adds control using language.

Campanile -> “a rocket ship”

i_start = 1	i_start = 3	i_start = 5	i_start = 7

i_start = 10	i_start = 20	i_start = 30	Original Image

Octocat -> “a photo of a dog”

i_start = 1	i_start = 3	i_start = 5	i_start = 7

i_start = 10	i_start = 20	i_start = 30	Original Image

Hoover Tower -> “a rocket ship”

i_start = 1	i_start = 3	i_start = 5	i_start = 7

i_start = 10	i_start = 20	i_start = 30	Original Image

5A Part 1.8: Visual Anagrams

In this part, we are going to implement Visual Anagrams. We will create an image that looks like something else when flipped upside down. The only modification to the original iterative denoising is that we will calculate $\epsilon$ as follows: $$ \epsilon_1 = \text{UNet}(x_t, t, p_1) $$ $$ \epsilon_2 = \text{flip}(\text{UNet}(\text{flip}(x_t), t, p_2)) $$ $$ \epsilon = (\epsilon_1 + \epsilon_2) / 2 $$

Original	Flipped
An Oil Painting of People Around a Campfire	An Oil Painting of an Old Man
An Oil Painting of a Snowy Mountain Village	An Oil Painting of People Around a Campfire
A Dreamy Oil Painting of a Crescent Moon Cradling a Sleeping Figure	An Ocean Wave Crashing Against a Lighthouse

5A Part 1.9: Hybrid Images

In this part, we are going to implement Factorized Diffusion and create hybrid images that look like one thing up close and another thing from far away. The only modification to the original iterative denoising is that we will calculate $\epsilon$ as follows: $$ \epsilon_1 = \text{UNet}(x_t, t, p_1) $$ $$ \epsilon_2 = \text{UNet}(x_t, t, p_2) $$ $$ \epsilon = f_\text{lowpass}(\epsilon_1) + f_\text{highpass}(\epsilon_2) $$

Image	Description (Low Frequency)	Description (High Frequency)
	Lithograph of a Skull	Waterfalls
	Ancient Clock Face	Historical Moments
	Oil Painting of an Old Man	Snowy Mountain Village

5A Bells & Whistles: A Course Logo

In this part, we are going to design a course logo using the diffusion model with prompt “A man whose head is a camera of brand CS180”.

The man in the logo looks cool! However, the CS180 brand is not on the camera (it might be caused by the word CS180 is not shown in the training data).

5B Part 1: Training a Single-Step Denoising UNet

In this part, we are going to train a single-step denoising UNet to denoise the digits in the MNIST dataset. Firstly, we will need to implement the noising process defined as follows: $$ z = x + \sigma \epsilon,\quad \text{where }\epsilon \sim N(0, I) $$

Then we will train a single-step denoising UNet to denoise the noisy digits at $\sigma = 0.5$.

We can see that the denoising UNet can denoise the noisy digits effectively after 5 epochs of training. However, what if we let it denoise the digits with different levels of noise that it was not trained on?

We can see that the denoising UNet cannot denoise the digits effectively with noise levels that it was not trained on, especially when the noise level is high.

5B Part 2.1: Adding Time-Conditioning to UNet

In this part, we are going to add time-conditioning to the UNet, making it a diffusion model. Firstly, we will add the noise with the following equation: $$ x_t = \sqrt{\bar\alpha_t} x_0 + \sqrt{1 - \bar\alpha_t} \epsilon \quad \text{where}~ \epsilon \sim N(0, 1) $$ And our objective is to minimize the following loss function: $$ L = \mathbb{E}_{\epsilon,x_0,t} |\epsilon_{\theta}(x_t, t) - \epsilon|^2 $$

After training the diffusion model, we can sample high-quality digits from the model iteratively.

5B Part 2.4: Adding Class-Conditioning to UNet

In this part, we are going to add class-conditioning to the UNet, enabling us to specify the which digit we want to generate.

After training the class-conditioned diffusion model, we choose which digit to generate and sample high-quality digits from the model iteratively.

5B Bells & Whistles: Sampling Gifs

This part has already been completed in the previous parts.